https://docs.google.com/presentation/d/17PAaBMnx-YsEfaTiw8DDw0PCUG14oW99/edit?usp=sharing&ouid=111622689205598921330&rtpof=true&sd=true
2. Повторити основні означення
3. Готувати відповіді на контрольні запитання 1-17 (ст. 26)
4. Виконати самостійну роботу і надіслати на пошту
5. Опрацювати відео урок
https://www.youtube.com/watch?v=-rkQgOmfZxs&ab_channel=%D0%A0%D0%BE%D0%B7%D0%B0%D0%A7%D0%B5%D1%80%D0%B5%D0%B2%D0%BA%D0%BE
Тема. Найбільше і найменше значення функції на проміжку.
Контрольна робота № 5
https://docs.google.com/presentation/d/1v6AzC-pBQts-qT18JiP8jbHaLa7wGgK2/edit?usp=sharing&ouid=111622689205598921330&rtpof=true&sd=true
2. Приклади записати в домашній зошит
3. Виконати контрольну роботу і надіслати на пошту
4. Опрацювати відео урок
https://www.youtube.com/watch?v=T7TkWFK2f9Y&ab_channel=%D0%A2%D0%BE%D0%BF%D0%A8%D0%BA%D0%BE%D0%BB%D0%B0
https://docs.google.com/presentation/d/19lEjBPLUjpWnFQPVnHEu5RBGt3lzqXHL/edit?usp=sharing&ouid=111622689205598921330&rtpof=true&sd=true
2. Записати всі приклади в домашній зошит
3. Опрацювати відео урок
https://www.youtube.com/watch?v=KbxwehihPPk&ab_channel=%D0%A2%D0%BE%D0%BF%D0%A8%D0%BA%D0%BE%D0%BB%D0%B0
03.05.2022
Тема. Точки екстремуму функції
1. Опрацювати параграф 22, презентацію
https://docs.google.com/presentation/d/1q8x1hAzZY-RVlM3vIYirwZL5yySW2swX/edit?usp=sharing&ouid=111622689205598921330&rtpof=true&sd=true
2. Конспект записати в зошит для конспектів
3. Завдання з презентації записати в зошит для домашніх робіт
4. Опрацювати відео урок
https://www.youtube.com/watch?v=ljf_smHsKVM&ab_channel=%D0%A2%D0%BE%D0%BF%D0%A8%D0%BA%D0%BE%D0%BB%D0%B0
Тема. Ознаки сталості,
зростання та спадання функції
1. Опрацювати параграф 21, презентацію
https://docs.google.com/presentation/d/1NfVrLcA-Qt1y6IvH9UYPDxsZOqmyMOy0/edit?usp=sharing&ouid=111622689205598921330&rtpof=true&sd=true2. Всі приклади в презентації, записати в зошит для домашніх робіт
3. Виконати домашню роботу і надіслати в “Єдину школу”
4. Опрацювати відео урокhttps://www.youtube.com/watch?v=cU2BRN-WuKc&ab_channel=%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0%D0%A1%D1%82%D0%B0%D1%81%D0%94%D0%BC%D0%B8%D1%82%D1%80%D0%BE%D0%B2%D0%B8%D1%87%D0%92%D0%BE%D0%BB%D1%8C%D0%B2%D0%B0%D1%87
https://docs.google.com/presentation/d/1ImoPBdyM_uIDWlDZF8Dv4m_cF_9vrd82/edit?usp=sharing&ouid=111622689205598921330&rtpof=true&sd=true
2. Опрацювати відео урок
https://www.youtube.com/watch?v=BlhIHh5_RNY&ab_channel=%D0%A2%D0%BE%D0%BF%D0%A8%D0%BA%D0%BE%D0%BB%D0%B0
3. Виконати самостійну роботу і надіслати в «Єдину школу»
Основні методи розв’язування ірраціональних рівнянь
Ірраціональними називаються рівняння, у якиx змінна міститься під знаком кореня (радикала) або під знаком піднесення до дробового степеня.
В окремих випадках, не розв’язуючи дане ірраціональне рівняння, можна встановити, що воно не має коренів. Наприклад, рівняння 
не має коренів, бо арифметичний корінь не може бути від’ємним.
Рівняння 
не має розв’язків, бо обидва доданки є арифметичними коренями, а тому не можуть бути від’ємними. А сума двох невід’ємних чисел дорівнює нулю лише тоді, коли кожен доданок дорівнює нулю. Одночасно ж вирази 
і 
нулю дорівнювати не можуть.
Основними методами розв’язування ірраціональних рівнянь є метод піднесення обох частин рівняння до одного і того самого степеня та метод введення нових змінних.
При розв’язуванні ірраціональних рівнянь методом піднесення обох частин до парного степеня можуть з’явитися побічні корені. Це відбувається за рахунок того, що при піднесенні обох частин початкового рівняння 
до парного степеня дістаємо рівняння, що є результатом не тільки рівняння 
, але і рівняння 
, оскільки і 
, і 
. Так, наприклад, візьмемо рівняння 
. Піднісши обидві частини цього рівняння до квад-рата, дістанемо 
Коренями цього рівняння є числа 
Однак після перевірки переконуємось, що 
є коренем рівняння , а 
є побічним коренем.
Приступаючи до розв’язання ірраціонального рівняння, що містить парні степені радикалів, буває корисним знаходження області допустимих значень (ОДЗ), це, як правило, полегшує розв’язування рівняння. Якщо робити лише еквівалентні перетворення, то перевірку робити не потрібно.
Розглянемо рівняння виду 
. Очевидно, що ліва частина рівняння, яка містить радикал парного степеня, не може бути від’ємна, а отже невід’ємна і права частина даного рівняння. Враховуючи область допустимих значень, підкореневий вираз також не може бути від’ємним. Отже, рівняння виду рівносильне такій системі:
.
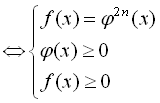Приклад 1. Розв’язати рівняння 
.
Розв’язання
Дане рівняння можна звести до вигляду 
, тобто 
.
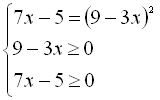
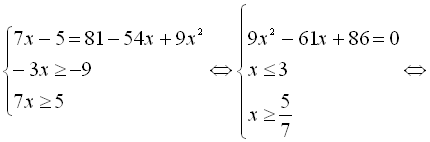
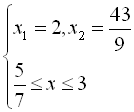З даної системи випливає, що лише 
є коренем початкового рівняння.
Відповідь: 
.
Приклад 2. Розв’язати рівняння 
.
Розв’язання
Область визначення даного рівняння визначається в результаті розв’-
язання системи нерівностей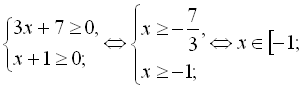 
.
Перетворимо дане рівняння:
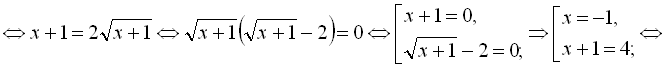
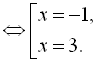
Обидва знайдені корені належать ОДЗ.
Відповідь: 
.
Приклад 3. Розв’язати рівняння 
.
Розв’язання
Знайдемо для початку область допустимих значень: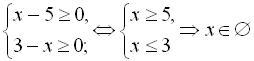 
.
Оскільки область допустимих значень виявилась пустою множиною, то і розв’язків дане рівняння не має.
Відповідь: 
.
4. Виконай самостіну роботу до 16.102021 р. і розвя’язки надішли за адресою l.v.antipina@gmail.com
11.10.2021
Тема. Корінь n-го степеня. Арифметичний корінь n-го степеня
1. Вивчити параграф 3, стор. 26-30
2. Опрацювати презентацію
https://docs.google.com/presentation/d/1B_PclXWXiGvRh58B5dbKdWxRsJXQJd1Q/edit?usp=sharing&ouid=111622689205598921330&rtpof=true&sd=true
3. Виконати № 3.2; 3.5; 3.7; 3.10, 3.12
sin2 α + cos2 α = 1
tg α · ctg α = 1
|
1 + tg2 α = |
1 |
|
cos2 α |
|
1 + ctg2 α = |
1 |
|
sin2 α |
Тригонометричні формули додавання
sin(α + β) = sin α · cos β + cos α ·
sin β
sin(α – β) = sin α · cos β – cos α ·
sin β
cos(α + β) = cos α · cos β – sin α ·
sin β
cos(α – β) = cos α · cos β + sin α ·
sin β
|
tg(α + β) = |
tg α + tg β |
|
1 – tgα · tg β |
|
tg(α – β) = |
tg α – tg β |
|
1 + tgα · tg β |
|
ctg(α + β) = |
ctgα · ctg β - 1 |
|
ctg β + ctg α |
|
ctg(α - β) = |
ctgα · ctg β + 1 |
|
ctg β - ctg α |
Формули пониження степеня
|
sin2 α = |
1 - cos 2α |
|
2 |
|
cos2 α = |
1 + cos 2α |
Формули перетворення суми і різниці тригонометричних
функцій на добуток
|
sin α +
sin β = 2 sin |
α + β |
cos |
α - β |
|
2 |
2 |
|
sin α -
sin β = 2 sin |
α - β |
cos |
α + β |
|
2 |
2 |
|
cos α +
cos β = 2 cos |
α + β |
cos |
α - β |
|
2 |
2 |
|
cos α -
cos β = -2 sin |
α + β |
sin |
α - β |
|
2 |
2 |
|
tg α + tg β = |
sin(α + β) |
|
cos α · cos β |
|
tg α - tg β = |
sin(α - β) |
|
cos α · cos β |
Формули перетворення добутку на суму
|
sin α · sin β = |
1 |
(cos(α - β) - cos(α + β)) |
|
2 |
|
sin α · cos β = |
1 |
(sin(α + β) + sin(α - β)) |
|
2 |
|
cos α · cos β = |
1 |
(cos(α + β) + cos(α - β)) |
|
2 |
Тема. Властивості тригонометричних функцій
1. Виконати тестові завдання
https://docs.google.com/forms/d/1MR45Dv-uStoarnWNnTzUiVxcd1rkiIhrYbP4ROyltW0/edit
Тести виконати 19.01 з 10.00 до 10.45
2. Опрацювати презентацію
https://docs.google.com/presentation/d/1e42yZ6tdPDLRF_TJ7dLWIoo7_i2GZK26Bg4WEMMmw30/edit?usp=sharing
3. Вивчити параграф 9
1. Область визначення тригонометричних функцій
2.Множина значень тригонометричних функцій
3.Знаки тригонометричних функцій
4.Парність і непарність тригонометричних функцій
5.Періодичність тригонометричних функцій
4. Якщо виникнуть ускладнення, то подивись відео урок https://www.youtube.com/watch?v=4YSWojA-yLE&ab_channel
Тема.Синус, косинус, тангенс і котангенс кута
1. Вивчити параграф 7,8
2. Означення синуса, косинуса, тангенса і котангенса
3. Тригонометричні значення деяких кутів
4. Знаходження тригонометричних значень за допомогою калькулятора
5. Радіанне вимірвання кутів
6. Тригонометричні функції числового аргумнта
2. Опрацювати презентацію https://docs.google.com/presentation/d/1gyE5W8qyibFoSSdVpUKxHJCt8j3l6s4-SsGA6W3KV7g/edit?usp=sharing
3. Опрацювати відео урок https://www.youtube.com/watch?v=xI_pTqHrUA8&ab_channel
(тема дуже важлива, тому обов’язково записати все в зошити для конспект
22.12.2020
Тема. Ірраціональні нерівності
Виконати самостійну роботу, надіслата за посиланням l.v.antipina@gmail.com
Опрацювати відео урок
https://www.youtube.com/watch?v=onR-bXurfLA&ab_channel=MONUKRAINE
Записати всі приклади в зошит для підготовки до ЗНО
15.12.2020
Тема. Контрольна робота. Степінь із раціональним показником. Степенева функція
1.Виконайте контрольну роботу на листочках до 17.00, 15.12.2020 і відправте
на електронну пошту l.v. antipina@gmail.com
20.10. 2020
Тема. Корінь n - го степеня. Арифметичний корінь n - го степеня
1. Вивчити параграф 3
2. Опрацювати презентацію
https://drive.google.com/file/d/1B_PclXWXiGvRh58B5dbKdWxRsJXQJd1Q/view?usp=sharing
3. В зошит для конспектів записати конспект
4. Подивись відео урок https://www.youtube.com/watch?v=z5KZfZgszpc&ab_channel=%D0%A2%D0%BE%D0%BF%D0%A8%D0%BA%D0%BE%D0%BB%D0%B0
11.10.2020
Математична олімпіада
Завдання І (шкільного) етапу Всеукраїнських учнівських олімпіад з математики
І частина містить 3 завдань у тестовій формі. За кожне виконане завдання нараховується 0-2 бали. Загальна кількість балів – 6.
ІІ частина містить 4 завдання з повним розв’язком задач. За кожне виконане завдання нараховується 6 балів.
Загальна кількість балів – 30
1. Уважно прочитайте умови задач і визначте порядок, в якому будете їх розв‘язувати (краще починати з легших задач, які, як правило, розміщені на початку).
2. Якщо неясно, чи правильне деяке твердження, спробуйте його довести або спростувати.
3. Не зациклюйтесь на одній задачі. Якщо немає ідеї розв‘язання, то задачу краще (хоча б на деякий час) відкласти.
4. Розв‘язавши задачу, зразу ж оформляйте розв‘язання. Це допоможе перевірити його правильність і звільнить увагу для інших задач.
5. Кожен, навіть очевидний, крок розв‘язання потрібно записувати. Громіздкі розв‘язання краще записувати у вигляді кількох тверджень (лем).
6. Перед тим, як здати роботу, уважно перечитайте її ―очима членів журі‖ — чи зможуть вони в ній розібратись?
Бажаю успіхів.
15.09.2020
Алгебра
Урок 3,4
Тема. Способи задання числових функцій
1. Вивчити параграф 1
2. Записати в зошит для домашніх робіт приклади задач, які розглядаються в параграфі 1
3. Виконати тестові завдання https://naurok.com.ua/test/join?gamecode=2847449
Виконати 15.09.2020, до 16.00 за 40 хвилин, спроба одна
08.09.2020
Алгебра
Урок №1
Добрий день!
2. Опрацюй презентацію
Комментариев нет:
Отправить комментарий